Améliorer vos régulateurs PID

Publié par Christophe Chaudelet le

Introduction

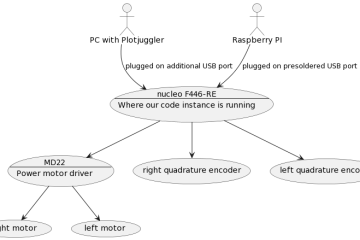
Le régulateur PID, appelé aussi correcteur PID (proportionnel, intégral, dérivé) est un système de contrôle permettant d’améliorer les performances d’un asservissement, c’est-à-dire un système ou procédé en boucle fermée. C’est le régulateur le plus utilisé dans l’industrie où ses qualités de correction s’appliquent à de multiples grandeurs physiques.

Parallèlement à l’étude de la bibliothèque Arduino PID, j’ai trouvé cette référence en anglais sur les PID. Cette dernière bibliothèque, bien que solide, n’était pas vraiment accompagnée d’une explication de code. Le but ici consiste à expliquer en détail pourquoi le code est tel qu’il est. J’espère que cela sera utile à deux groupes de personnes :

  • Les personnes directement intéressées par ce qui se passe dans la bibliothèque Arduino PID, elles recevront une explication détaillée.
  • Quiconque qui écrit son propre algorithme PID, il pourra jeter un œil et emprunter ce qu’il souhaite pour améliorer son correcteur PID.

Voici le travail de traduction des explications du code de brettbeauregard.com.

On va commencer par ce qu’on appelle “le PID du débutant“. On va ensuite l’améliorer étape par étape jusqu’à ce qu’il nous reste un algorithme PID efficace et robuste.

Le PID du débutant

Voici l’équation PID telle que tout le monde l’apprend pour la première fois :

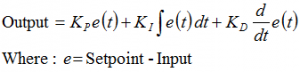
Cela conduit à peu près tout le monde à écrire le contrôleur PID suivant :
<code>/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
void Compute()
{
   /*How long since we last calculated*/
   unsigned long now = millis();
   double timeChange = (double)(now - lastTime);
  
   /*Compute all the working error variables*/
   double error = Setpoint - Input;
   errSum += (error * timeChange);
   double dErr = (error - lastErr) / timeChange;
  
   /*Compute PID Output*/
   Output = kp * error + ki * errSum + kd * dErr;
  
   /*Remember some variables for next time*/
   lastErr = error;
   lastTime = now;
}
  
void SetTunings(double Kp, double Ki, double Kd)
{
   kp = Kp;
   ki = Ki;
   kd = Kd;
}</code>
Langage du code : C++ (cpp)

Compute() est appelé régulièrement ou irrégulièrement, et cela fonctionne plutôt bien.

SOMMAIRE

Si nous voulons transformer ce code en quelque chose d’équivalent aux contrôleurs PID industriels, nous devrons régler quelques points:

  • Temps d’échantillonnage – L’algorithme PID fonctionne mieux s’il est évalué à intervalles réguliers. Si l’algorithme est conscient de cet intervalle, nous pouvons également simplifier certains calculs internes.
  • Pic de dérivée (Derivative Kick) – Ce n’est pas le plus gros problème, mais il est facile de s’en débarrasser.
  • Changements de réglage à la volée – Un bon algorithme PID est un algorithme dans lequel les paramètres de réglage peuvent être modifiés sans modifier le fonctionnement interne.
  • Réinitialiser la saturation d’intégrale (Reset Windup) – Nous verrons ce qu’est la réinitialisation de la saturation d’intégrale et mettrons en œuvre une solution avec des avantages secondaires.
  • Marche/Arrêt (Auto/Manuel) – Dans la plupart des applications, on souhaite parfois éteindre le contrôleur PID et régler la sortie à la main, sans que le contrôleur n’interfère.
  • Initialisation – Lorsque le contrôleur s’allume pour la première fois, nous voulons un “transfert sans à-coups”. Autrement dit, nous ne voulons pas que la sortie passe soudainement à une nouvelle valeur.
  • Direction du contrôleur – Ce dernier n’est pas un changement au nom de la robustesse en soi. il est conçu pour s’assurer que l’utilisateur saisit les paramètres de réglage avec le bon signe.
  • En option: Proportionnel à la mesure – L’ajout de cette fonctionnalité facilite le contrôle de certains types de processus.

Une fois que nous aurons résolu tous ces problèmes, nous aurons un algorithme PID solide. Nous aurons également, sans coïncidence, le code utilisé dans la dernière version de la bibliothèque Arduino PID. Donc, que vous essayiez d’écrire votre propre algorithme ou que vous essayiez de comprendre ce qui se passe dans la bibliothèque PID, j’espère que cela vous aidera.

NB: Dans tous les exemples de code, j’utilise des doubles. Sur l’Arduino, un type double est identique à un type float (simple précision). La vraie double précision est un petit peu “overkill” pour un PID. Si le langage que vous utilisez fait une vraie double précision, on vous recommande de changer tous les doubles en flottants (float).

1. Temps d’échantillonnage (Sample Time)

Le problème

Le PID du débutant est conçu pour être appelé de manière irrégulière. Cela cause 2 problèmes :

  • Vous n’obtenez pas un comportement cohérent du PID, car parfois il est appelé fréquemment et parfois non.
  • Vous devez faire des calculs supplémentaires en calculant la dérivée et l’intégrale, car elles dépendent toutes deux du changement de temps.

La solution

Assurez-vous que le PID est appelé à intervalles réguliers. La façon dont j’ai décidé de le faire est de spécifier que la fonction de calcul est appelée à chaque cycle. sur la base d’un temps d’échantillonnage prédéterminé, le PID décide s’il doit calculer ou revenir immédiatement.

Une fois que nous savons que le PID est évalué à un intervalle constant, les calculs de dérivée et d’intégrale peuvent également être simplifiés. Bonus!

Le code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastErr;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      errSum += error;
      double dErr = (error - lastErr);
 
      /*Compute PID Output*/
      Output = kp * error + ki * errSum + kd * dErr;
 
      /*Remember some variables for next time*/
      lastErr = error;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
Langage du code : C++ (cpp)

Aux lignes 10 et 11, l’algorithme décide maintenant par lui-même s’il est temps de calculer. De plus, parce que nous savons maintenant que ce sera le même temps entre les échantillons, nous n’avons pas besoin de multiplier constamment par le changement de temps. Nous pouvons simplement ajuster le Ki et le Kd de manière appropriée (lignes 31 et 32) et le résultat est mathématiquement équivalent, mais plus efficace.

Une petite attention tout de même avec cette façon de faire: si l’utilisateur décide de modifier le temps d’échantillonnage pendant le fonctionnement, le Ki et le Kd devront être modifiés pour refléter ce nouveau changement. C’est de cela qu’il s’agit aux lignes 39 à 42.

Notez également qu’on convertit le temps d’échantillonnage en secondes sur la ligne 29. Strictement parlant, ce n’est pas nécessaire, mais permet à l’utilisateur d’entrer Ki et Kd en unités de 1/sec et s, plutôt que 1/ms et ms.

Le Résultat

Les changements ci-dessus font 3 choses pour nous:

  1. Quelle que soit la fréquence d’appel de Compute(), l’algorithme PID sera évalué à intervalles réguliers [Ligne 11]
  2. En raison de la soustraction de temps [Ligne 10], il n’y aura aucun problème lorsque millis() revient à 0. Cela ne se produit que tous les 55 jours, mais nous optons pour l’épreuve des balles, souvenez-vous ?
  3. Nous n’avons plus besoin de multiplier et de diviser par le changement d’heure. Puisqu’il s’agit d’une constante, nous pouvons la déplacer du code de calcul [lignes 15+16] et la regrouper avec les constantes de réglage [lignes 31+32]. Mathématiquement, cela revient au même, mais cela enregistre une multiplication et une division à chaque fois que le PID est évalué.

Note sur les interruptions

Si ce PID va dans un microcontrôleur, un très bon argument peut être avancé pour utiliser une interruption. SetSampleTime() définit la fréquence d’interruption, puis Compute() est appelé au moment opportun. Il n’y aurait pas besoin, dans ce cas, des lignes 9-12, 23 et 24. Si vous envisagez de le faire avec votre implémentation PID, allez-y ! Continuez à lire cette série cependant. Nous espérons que vous bénéficierez encore des modifications qui suivent.
Il y a trois raisons pour lesquelles on n’a pas utilisé les interruptions:

  1. En ce qui concerne cette série, tout le monde ne pourra pas utiliser les interruptions.
  2. Les choses deviendraient délicates si vous vouliez qu’il implémente plusieurs contrôleurs PID en même temps.

2. Pic de dérivé (Derivative Kick)

Le problème

Cette modification va modifier un peu le terme dérivé. Le but est d’éliminer un phénomène connu sous le nom de “Derivative Kick”.

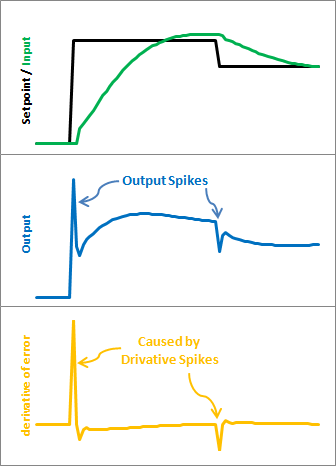
[Exemple de Pic de dérivé – Derivative Kick]

L’image ci-dessus illustre le problème. Comme error=Setpoint-Input, tout changement de Setpoint provoque un changement instantané d’erreur. La dérivée de ce changement est l’infini (en pratique, puisque dt n’est pas 0, il finit par être un très grand nombre). Ce nombre est introduit dans l’équation du pid, ce qui entraîne une pointe indésirable dans la sortie. Heureusement, il existe un moyen facile de s’en débarrasser.

La Solution

Il s’avère que la dérivée de l’erreur est égale à la dérivée négative de l’entrée, SAUF lorsque le point de consigne change. Cela finit par être une solution parfaite. Au lieu d’ajouter (Kd * dérivée de l’Erreur), nous soustrayons (Kd * dérivée de l’Entrée). C’est ce qu’on appelle l’utilisation de “dérivée sur mesure” (“Derivative on Measurement”).

Le Code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double errSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      errSum += error;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ki * errSum - kd * dInput;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
Langage du code : JavaScript (javascript)

Le Résultat

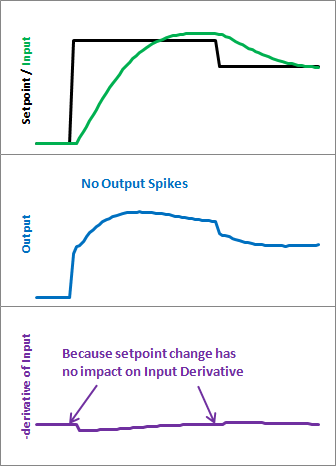
[Résultat de correction du Pic de dérivé – Derivative Kick]

Voici ce que ces modifications nous apportent. Notez que l’entrée semble toujours à peu près la même. Nous obtenons donc les mêmes performances, mais nous n’envoyons pas un énorme pic de sortie à chaque fois que le point de consigne change.

Cela peut ou peut ne pas être un gros problème. Tout dépend de la sensibilité de votre application aux pics de sortie.

3. Changements de réglage à la volée

Le Problème

La possibilité de modifier les paramètres de réglage pendant que le système est en cours d’exécution est indispensable pour tout algorithme PID respectable.

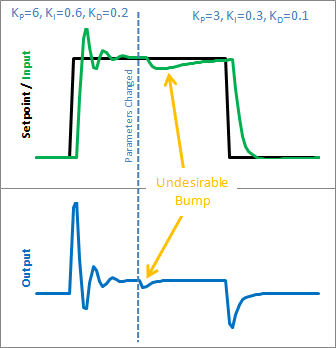
[Exemple de changements de réglage à la volée]

Le PID du débutant agit un peu fou si vous essayez de changer les réglages pendant qu’il est en cours d’exécution. Voyons pourquoi. Voici l’état du PID du débutant avant et après le changement de paramètre ci-dessus :

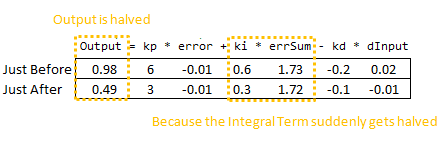
[Cas du changement du paramètre Intégrale]

Nous pouvons donc immédiatement blâmer cette bosse sur le terme intégral. C’est la seule chose qui change radicalement lorsque les paramètres changent. Pourquoi est-ce arrivé? Cela a à voir avec l’interprétation du débutant de l’intégrale :

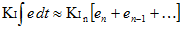
Cette interprétation fonctionne bien jusqu’à ce que le Ki soit changé. Puis, tout d’un coup, vous multipliez ce nouveau Ki par la totalité de la somme d’erreurs que vous avez accumulée. Ce n’est pas ce que nous voulions ! Nous voulions seulement affecter les choses pour aller de l’avant !

La Solution

Il y a plusieurs façons de résoudre ce problème. La méthode utilisée dans la dernière bibliothèque consistait à redimensionner errSum. Ki doublé ? Couper errSum en deux. Cela empêche le terme I de se cogner, et cela fonctionne. C’est un peu maladroit cependant, et il y a quelque chose de plus élégant.

La solution nécessite un peu d’algèbre de base (^^)

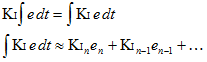
Au lieu d’avoir le Ki vivant à l’extérieur de l’intégrale, nous l’amenons à l’intérieur. On dirait que nous n’avons rien fait, mais nous verrons qu’en pratique, cela fait une grande différence.

Maintenant, nous prenons l’erreur et la multiplions par le Ki à ce moment-là. Nous stockons ensuite la somme de cela. Lorsque le Ki change, il n’y a pas de bosse car tous les anciens Ki sont déjà “dans la banque” pour ainsi dire. Nous obtenons un transfert fluide sans opérations mathématiques supplémentaires.

Le Code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
void Compute()
{
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm += (ki * error);
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm - kd * dInput;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
Langage du code : C++ (cpp)

Nous avons donc remplacé la variable errSum par une variable composite ITerm [Ligne 4]. Il additionne Ki*error, plutôt qu’une simple erreur [Ligne 15]. De plus, comme Ki est maintenant enterré dans ITerm, il est supprimé du calcul principal du PID [Ligne 19].

Le Résultat

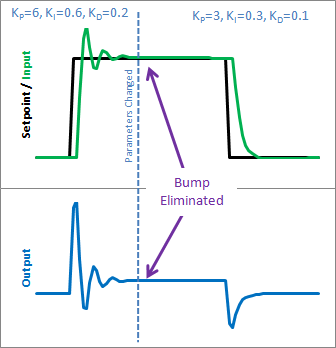
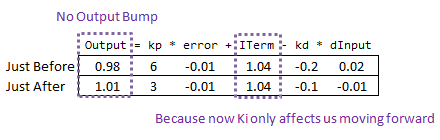
[Résultat de la solution au changements de réglage à la volée]
[Résultat de la solution sur le Ki]

Alors, comment cela résout-il les choses. Avant, lorsque ki était modifié, il remettait à l’échelle la somme totale de l’erreur ; chaque valeur d’erreur que nous avions vue. Avec ce code, l’erreur précédente reste intacte et le nouveau ki n’affecte que les choses qui avancent, ce qui est exactement ce que nous voulons.

4. Réinitialiser la saturation d’intégrale (Reset Windup)

Le Problème

[Le problème de la saturation d’intégrale]

La réinitialisation de la saturation d’intégrale est un piège qui réclame probablement plus de questions des débutants. Cela se produit lorsque le PID pense qu’il peut faire quelque chose qu’il ne peut pas faire. Par exemple, la sortie PWM sur un Arduino accepte des valeurs de 0 à 255. Par défaut, le PID ne le sait pas. S’il pense que 300-400-500 fonctionnera, il essaiera ces valeurs en espérant obtenir ce dont il a besoin. Puisqu’en réalité la valeur est fixée à 255, il va juste continuer à essayer des nombres de plus en plus élevés sans aller nulle part.

Le problème se révèle sous la forme de décalages étranges. Ci-dessus, nous pouvons voir que la sortie est “enroulée” bien au-dessus de la limite externe. Lorsque le point de consigne est abaissé, la sortie doit se ralentir avant de descendre en dessous de cette ligne 255.

La Solution – étape 1

[Etape 1 de la solution de saturation d’intégrale]

Il existe plusieurs façons d’atténuer la saturation, mais celle qu’on a choisie était la suivante : indiquez au PID quelles sont les limites de sortie. Dans le code ci-dessous, vous verrez qu’il y a maintenant une fonction SetOuputLimits. Une fois que l’une ou l’autre limite est atteinte, le pid arrête d’additionner (d’intégrer). Il sait qu’il n’y a rien à faire ; Étant donné que la sortie ne s’enroule pas, nous obtenons une réponse immédiate lorsque le point de consigne tombe dans une plage où nous pouvons faire quelque chose.

La Solution – étape 2

Notez cependant dans le graphique ci-dessus que même si nous nous sommes débarrassés de ce retard de saturation, nous n’en sommes pas encore là. Il y a toujours une différence entre ce que le pid pense envoyer et ce qui est envoyé. Pourquoi? le terme Proportionnelle et (dans une moindre mesure) le terme Dérivée.

Même si le terme Intégral (I-Term) a été bloqué en toute sécurité, P et D ajoutent toujours leurs deux valeurs, donnant un résultat supérieur à la limite de sortie. A mon sens, c’est inacceptable. Si l’utilisateur appelle une fonction appelée “SetOutputLimits”, il doit supposer que cela signifie que “la sortie restera dans ces valeurs”. Donc, pour l’étape 2, nous en faisons une hypothèse valide. En plus de bloquer le “I-Term”, nous bloquons la valeur de sortie afin qu’elle reste là où nous l’attendons.

(Remarque : Vous pourriez vous demander pourquoi nous devons serrer les deux. Si nous devons de toute façon resserrer la sortie, pourquoi resserrer l’intégrale séparément ? Si tout ce que nous avons fait était de resserrer la sortie, le terme d’intégrale reviendrait à croître et à croître. Bien que la sortie ait l’air bien pendant l’étape, nous verrions ce décalage révélateur lors de la descente.)

Le Code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
void Compute()
{
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm> outMax) ITerm= outMax;
      else if(ITerm< outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
 
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
    
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;
}
Langage du code : C++ (cpp)

Une nouvelle fonction a été ajoutée pour permettre à l’utilisateur de spécifier les limites de sortie [lignes 52-63]. Et ces limites sont utilisées pour serrer à la fois le I-Term [17-18] et la sortie [23-24]

Le Résultat

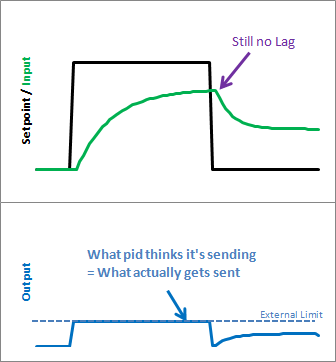
[Résultat de la solution de saturation d’intégrale]

Comme nous pouvons le voir, la saturation est éliminée. Dplus, la sortie reste là où nous le voulons. cela signifie qu’il n’y a pas besoin de resserrage externe de la sortie. Si vous voulez qu’il soit compris entre 23 et 167, vous pouvez les définir comme limites de sortie.

5. PID Marche/Arrêt (Auto/Manuel)

Le Problème

Aussi agréable qu’il soit d’avoir un contrôleur PID, parfois vous ne vous souciez pas de ce qu’il a à dire.

[Problème lié au PID ON/OFF]

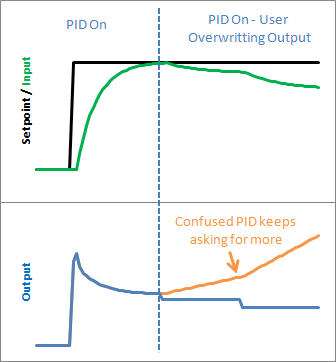
Supposons qu’à un moment donné de votre programme vous souhaitiez forcer la sortie à une certaine valeur (0 par exemple), vous pouvez certainement le faire dans la routine d’appel :

void loop()
{
  Compute();
  Output=0;
}Langage du code : JavaScript (javascript)

De cette façon, peu importe ce que dit le PID, vous écrasez simplement sa valeur. C’est cependant une idée terrible dans la pratique, car le PID deviendra très confus : “On continue à déplacer la sortie et rien ne se passe ! Ce qui donne?! Déplaçons le encore un peu plus”. Par conséquent, lorsque vous arrêtez d’écraser la sortie et que vous revenez au PID, vous obtiendrez probablement un changement énorme et immédiat de la valeur de sortie.

La Solution

La solution à ce problème est d’avoir un moyen d’éteindre et d’allumer le PID. Les termes communs pour ces états sont “Manuel” (on ajustera la valeur à la main) et “Automatique” (le PID ajustera automatiquement la sortie). Voyons comment cela se fait dans le code :

Le Code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
 
#define MANUAL 0
#define AUTOMATIC 1
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm> outMax) ITerm= outMax;
      else if(ITerm< outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
 
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
    
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;
}
 
void SetMode(int Mode)
{
  inAuto = (Mode == AUTOMATIC);
}
Langage du code : C++ (cpp)

Une solution assez simple. Si vous n’êtes pas en mode automatique, quittez immédiatement la fonction Compute sans ajuster la sortie ou les variables internes.

Le Résultat

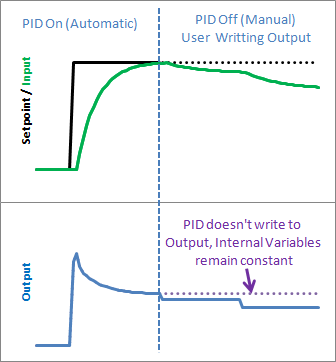
[Résultat de la solution au PID ON/OFF]

Il est vrai que vous pourriez obtenir un effet similaire en n’appelant simplement pas la fonction Compute() à partir de la routine d’appel, mais cette solution conserve le fonctionnement du PID contenu, ce qui est en quelque sorte ce dont nous avons besoin. En gardant les choses en interne, nous pouvons garder une trace du mode dans lequel nous nous trouvions et, plus important encore, cela nous permet de savoir quand nous changeons de mode. Cela nous amène au prochain chapitre…

6. Initialisation

Le Problème

Dans la dernière section, nous avons implémenté la possibilité d’activer et de désactiver le PID. Nous l’avons désactivé, mais regardons maintenant ce qui se passe lorsque nous le rallumons :

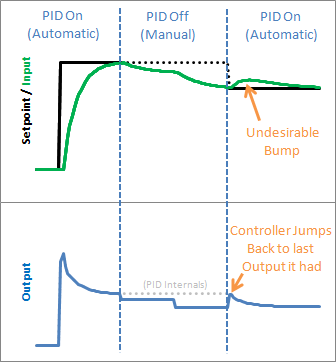
[Problème lié à l’initialisation du PID]

Aïe ! Le PID revient à la dernière valeur de sortie qu’il a envoyée, puis commence à s’ajuster à partir de là. Cela se traduit par une bosse d’entrée que nous préférerions ne pas avoir.

La Solution

Celui-ci est assez facile à réparer. Puisque nous savons maintenant quand nous allumons (en passant de Manuel à Automatique), nous n’avons plus qu’à initialiser les choses pour une transition en douceur. Cela signifie masser les 2 variables de travail stockées (ITerm & lastInput) pour empêcher la sortie de sauter.

Le Code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
 
#define MANUAL 0
#define AUTOMATIC 1
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm> outMax) ITerm= outMax;
      else if(ITerm< outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output> outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
 
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
    
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;
}
 
void SetMode(int Mode)
{
    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto && !inAuto)
    {  /*we just went from manual to auto*/
        Initialize();
    }
    inAuto = newAuto;
}
 
void Initialize()
{
   lastInput = Input;
   ITerm = Output;
   if(ITerm> outMax) ITerm= outMax;
   else if(ITerm< outMin) ITerm= outMin;
}
Langage du code : C++ (cpp)

Nous avons modifié la fonction SetMode(…) pour détecter le passage du manuel à l’automatique, et nous avons ajouté notre fonction d’initialisation. On définit ITerm=Output pour prendre en charge le terme intégral et lastInput = Input pour empêcher la dérivée de monter en flèche. Le terme proportionnel ne repose sur aucune information du passé, il n’a donc pas besoin d’initialisation.

Le Résultat

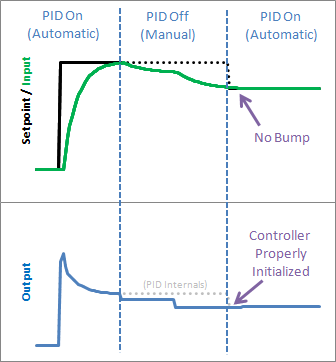
[Résultat de l’optimisation de l’initialisation du PID]

Nous voyons sur le graphique ci-dessus qu’une initialisation correcte se traduit par un transfert sans à-coups du manuel à l’automatique : exactement ce que nous recherchions.

Mise à jour : pourquoi pas ITerm=0 ?

Pourquoi on ne définit pas ITerm=0 lors de l’initialisation? En guise de réponse, il faut envisager le scénario suivant : le pid est en mode manuel et l’utilisateur a défini la sortie sur 50. Après un certain temps, le processus se stabilise à une entrée de 75,2. L’utilisateur fait le Setpoint à 75.2 et allume le pid. Que devrait-il se passer ?

On peut affirmer qu’après le passage en automatique, la valeur de sortie doit rester à 50. Puisque les termes P et D seront nuls, la seule façon pour que cela se produise est si ITerm est initialisé à la valeur de Output.

Si vous êtes dans cette situation, où vous avez besoin que la sortie s’initialise à zéro, il n’est pas nécessaire de modifier le code ci-dessus. Définissez simplement Output=0 dans votre routine d’appel avant de faire passer le PID de Manuel à Automatique.

7. Direction du contrôleur

Le Problème

Les processus auxquels le PID sera connecté se divisent en deux groupes : action directe et action inverse. Tous les exemples qu’on a montrés jusqu’à présent ont été des actions directes. Autrement dit, une augmentation de la sortie entraîne une augmentation de l’entrée. Pour les processus à action inverse, le contraire est vrai. Dans un réfrigérateur par exemple, une augmentation du refroidissement fait baisser la température. Pour faire fonctionner le PID débutant avec un processus inverse, les signes de kp, ki et kd doivent tous être négatifs.

Ce n’est pas un problème en soi, mais l’utilisateur doit choisir le bon signe et s’assurer que tous les paramètres ont le même signe.

La Solution

Pour rendre le processus un peu plus simple, j’exige que kp, ki et kd soient tous >=0. Si l’utilisateur est connecté à un processus inverse, il le spécifie séparément à l’aide de la fonction SetControllerDirection. Cela garantit que les paramètres ont tous le même signe et, espérons-le, rend les choses plus intuitives.

Le Code

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
 
#define MANUAL 0
#define AUTOMATIC 1
 
#define DIRECT 0
#define REVERSE 1
int controllerDirection = DIRECT;
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm > outMax) ITerm= outMax;
      else if(ITerm < outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
 
      /*Compute PID Output*/
      Output = kp * error + ITerm- kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
 
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
 
void SetTunings(double Kp, double Ki, double Kd)
{
   if (Kp<0 || Ki<0|| Kd<0) return;
 
  double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
 
  if(controllerDirection ==REVERSE)
   {
      kp = (0 - kp);
      ki = (0 - ki);
      kd = (0 - kd);
   }
}
 
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
 
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
 
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
 
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;
}
 
void SetMode(int Mode)
{
    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto == !inAuto)
    {  /*we just went from manual to auto*/
        Initialize();
    }
    inAuto = newAuto;
}
 
void Initialize()
{
   lastInput = Input;
   ITerm = Output;
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;
}
 
void SetControllerDirection(int Direction)
{
   controllerDirection = Direction;
}
Langage du code : C++ (cpp)

Le Résultat Complet

Et c’est à peu près tout. Nous avons transformé le PID du débutant (“The Beginner’s PID”) en un contrôleur beaucoup plus robuste. Pour les lecteurs qui cherchaient une explication détaillée de la bibliothèque PID, on espère que vous avez trouvé ce que vous cherchiez. Pour ceux d’entre vous qui écrivez votre propre PID, on espère que vous avez pu glaner quelques idées qui vous feront économiser quelques cycles de programmation et du temps.

Deux notes finales :

  1. Si quelque chose dans cette série semble incorrect, faites-le moi savoir. J’ai peut-être raté quelque chose, ou j’ai peut-être juste besoin d’être plus clair dans mon explication. En tout cas j’aimerais savoir.
  2. Ceci est juste un PID de base. Il y a beaucoup d’autres problèmes que j’ai intentionnellement laissés de côté au nom de la simplicité.

8. Proportionnel à la Mesure (Proportional on Measurement) – The Code

Les 3 passes ci-dessous détaillent comment j’ai procédé pour ajouter PonM à la bibliothèque PID.

Premier passage – Sélection de l’entrée initiale et du mode proportionnel

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
  
#define MANUAL 0
#define AUTOMATIC 1
  
#define DIRECT 0
#define REVERSE 1
int controllerDirection = DIRECT;
  
#define P_ON_M 0
#define P_ON_E 1
bool pOnE = true;
double initInput;
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
      /*Compute all the working error variables*/
      double error = Setpoint - Input;
      ITerm+= (ki * error);
      if(ITerm > outMax) ITerm= outMax;
      else if(ITerm < outMin) ITerm= outMin;
      double dInput = (Input - lastInput);
  
      /*Compute P-Term*/
      if(pOnE) Output = kp * error;
      else Output = -kp * (Input-initInput); 
 
      /*Compute Rest of PID Output*/
      Output += ITerm - kd * dInput;
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
  
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
  
void SetTunings(double Kp, double Ki, double Kd, int pOn)
{
   if (Kp<0 || Ki<0|| Kd<0) return;
  
   pOnE = pOn == P_ON_E;
   
   double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
  
  if(controllerDirection ==REVERSE)
   {
      kp = (0 - kp);
      ki = (0 - ki);
      kd = (0 - kd);
   }
}
  
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
  
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
  
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
  
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;
}
  
void SetMode(int Mode)
{
    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto == !inAuto)
    {  /*we just went from manual to auto*/
        Initialize();
    }
    inAuto = newAuto;
}
  
void Initialize()
{
   lastInput = Input;
   initInput = Input;
   ITerm = Output;
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;
}
  
void SetControllerDirection(int Direction)
{
   controllerDirection = Direction;
}
Langage du code : C++ (cpp)

La mesure proportionnelle offre une résistance croissante à mesure que l’entrée change, mais sans cadre de référence, nos performances seraient un peu bancales. Si l’entrée PID est de 10 000 lorsque nous allumons le contrôleur pour la première fois, voulons-nous vraiment commencer à résister avec Kp*10 000 ? Non. Nous voulons utiliser notre entrée initiale comme point de référence (ligne 108,) l’augmentation ou la diminution de la résistance à mesure que l’entrée change à partir de là (ligne 38.)

L’autre chose que nous devons faire est de permettre à l’utilisateur de choisir s’il veut faire Proportionnel sur erreur ou Mesure. Après le dernier message, il peut sembler que PonE est inutile, mais il est important de se rappeler que pour de nombreuses boucles, cela fonctionne bien. En tant que tel, nous devons laisser l’utilisateur choisir le mode qu’il souhaite (lignes 51 et 55), puis agir en conséquence dans le calcul (lignes 37 et 38).

Deuxième passe – Modifications de réglage à la volée

Bien que le code ci-dessus fonctionne effectivement, il a un problème que nous avons déjà vu. Lorsque les paramètres de réglage sont modifiés lors de l’exécution, nous obtenons un blip indésirable.

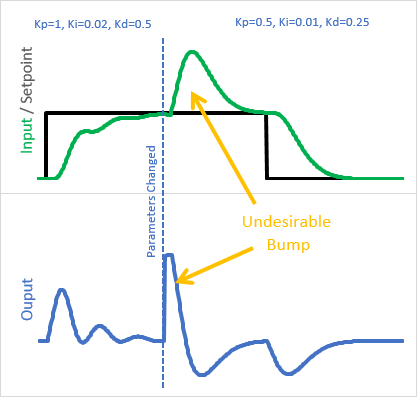
[Deuxième passe – Modifications de réglage à la volée]

Pourquoi cela arrive-t-il?

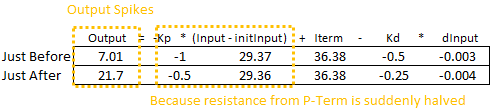
[Parce que la résistance du terme P est soudainement réduit de moitié]

La dernière fois que l’on a vu cela, c’était avec l’intégrale qui était remise à l’échelle par un nouveau Ki. Cette fois, c’est (Input – initInput) qui est redimensionné par Kp. La solution qu’on choisit est similaire à ce qu’on a fait pour Ki : au lieu de traiter l’entrée – initInput comme une unité monolithique multipliée par le Kp actuel, on l’a divisé en étapes individuelles multipliées par le Kp à ce moment là :

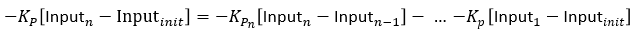
/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double ITerm, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
  
#define MANUAL 0
#define AUTOMATIC 1
  
#define DIRECT 0
#define REVERSE 1
int controllerDirection = DIRECT;
  
#define P_ON_M 0
#define P_ON_E 1
bool pOnE = true;
double PTerm;
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
    
      /*Compute all the working error variables*/      
      double error = Setpoint - Input;   
      ITerm+= (ki * error);  
      if(ITerm > outMax) ITerm= outMax;      
      else if(ITerm < outMin) ITerm= outMin;  
      double dInput = (Input - lastInput);
 
      /*Compute P-Term*/
      if(pOnE) Output = kp * error; 
      else 
      { 
         PTerm -= kp * dInput; 
         Output = PTerm; 
      } 
       
      /*Compute Rest of PID Output*/
      Output += ITerm - kd * dInput; 
    
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
  
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
  
void SetTunings(double Kp, double Ki, double Kd, int pOn)
{
   if (Kp<0 || Ki<0|| Kd<0) return;
  
   pOnE = pOn == P_ON_E;
   
   double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
  
  if(controllerDirection ==REVERSE)
   {
      kp = (0 - kp);
      ki = (0 - ki);
      kd = (0 - kd);
   }
}
  
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
  
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
  
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
  
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;
}
  
void SetMode(int Mode)
{
    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto == !inAuto)
    {  /*we just went from manual to auto*/
        Initialize();
    }
    inAuto = newAuto;
}
  
void Initialize()
{
   lastInput = Input;
   PTerm = 0;
   ITerm = Output;
   if(ITerm > outMax) ITerm= outMax;
   else if(ITerm < outMin) ITerm= outMin;
}
  
void SetControllerDirection(int Direction)
{
   controllerDirection = Direction;
}
Langage du code : C++ (cpp)

Au lieu de multiplier l’intégralité de l’Input-initInput par Kp, nous gardons maintenant une somme de travail, PTerm. À chaque étape, nous multiplions simplement le changement d’entrée actuel par Kp et le soustrayons de PTerm (ligne 41). Ici, nous pouvons voir l’impact du changement :

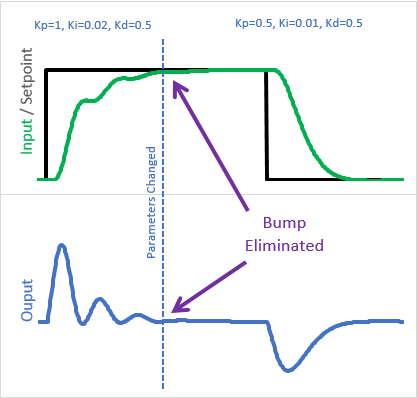
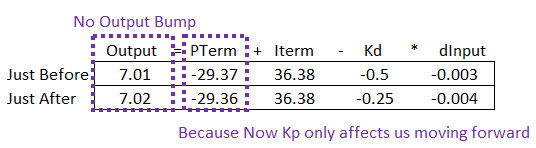
[Résultat de la deuxième passe – Modifications de réglage à la volée]
[Parce que maintenant Kp nous affecte uniquement en allant de l’avant]

Parce que les anciens Kps sont “dans la banque”, le changement des paramètres de réglage ne nous affecte que pour aller de l’avant.

Passe finale – Problèmes de somme.

On ne va pas entrer dans les détails complexes (à tendances fantaisistes, etc.) quant à ce qui ne va pas avec le code ci-dessus. C’est plutôt bien, mais il y a encore des problèmes majeurs avec ça. Par exemple:

  • “Windup”, en quelque sorte : bien que la sortie finale soit limitée entre outMin et outMax, il est possible que PTerm se développe alors qu’il ne le devrait pas. Ce ne serait pas aussi mauvais qu’une saturation intégrale, mais ce ne serait pas toujours acceptable.
  • Modifications à la volée : si l’utilisateur devait passer de P_ON_M à P_ON_E pendant l’exécution, puis après un certain temps, le PTerm ne serait pas initialisé et cela provoquerait une bosse de sortie.

Il y en a d’autres, mais ceux-ci suffisent pour voir quel est le véritable problème. Nous avons traité tout cela auparavant, lorsque nous avons créé ITerm. Plutôt que de passer en revue et de réimplémenter les mêmes solutions pour PTerm, on a opté pour une solution plus esthétique.

En fusionnant PTerm et ITerm en une seule variable appelée “outputSum”, le code P_ON_M bénéficie alors de tous les correctifs ITerm déjà en place, et comme il n’y a pas deux sommes dans le code, il n’y a pas de redondance inutile.

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double outputSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
  
#define MANUAL 0
#define AUTOMATIC 1
  
#define DIRECT 0
#define REVERSE 1
int controllerDirection = DIRECT;
  
#define P_ON_M 0
#define P_ON_E 1
bool pOnE = true;
 
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
    
      /*Compute all the working error variables*/      
      double error = Setpoint - Input;   
      double dInput = (Input - lastInput);
      outputSum+= (ki * error);  
       
      /*Add Proportional on Measurement, if P_ON_M is specified*/
      if(!pOnE) outputSum-= kp * dInput
       
      if(outputSum > outMax) outputSum= outMax;      
      else if(outputSum < outMin) outputSum= outMin;  
     
      /*Add Proportional on Error, if P_ON_E is specified*/
      if(pOnE) Output = kp * error; 
      else Output = 0;
       
      /*Compute Rest of PID Output*/
      Output += outputSum - kd * dInput; 
    
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
  
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
  
void SetTunings(double Kp, double Ki, double Kd, int pOn)
{
   if (Kp<0 || Ki<0|| Kd<0) return;
  
   pOnE = pOn == P_ON_E;
   
   double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
  
  if(controllerDirection ==REVERSE)
   {
      kp = (0 - kp);
      ki = (0 - ki);
      kd = (0 - kd);
   }
}
  
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
  
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
  
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
  
   if(outputSum > outMax) outputSum= outMax;
   else if(outputSum < outMin) outputSum= outMin;
}
  
void SetMode(int Mode)
{
    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto == !inAuto)
    {  /*we just went from manual to auto*/
        Initialize();
    }
    inAuto = newAuto;
}
  
void Initialize()
{
   lastInput = Input;
    
   outputSum = Output;
   if(outputSum > outMax) outputSum= outMax;
   else if(outputSum < outMin) outputSum= outMin;
}
  
void SetControllerDirection(int Direction)
{
   controllerDirection = Direction;
}
Langage du code : C++ (cpp)

Et voila. La fonctionnalité ci-dessus est ce qui est maintenant présent dans la v1.2.0 du PID Arduino.

Mais attendez, il y a plus : la pondération du point de consigne.

Le code qui suit n’a pas été ajouté à la bibliothèque Arduino, mais c’est une fonctionnalité qui pourrait être intéressante si vous voulez créer la vôtre. La pondération du point de consigne est, à la base, un moyen d’avoir à la fois PonE et PonM en même temps. En spécifiant un rapport entre 0 et 1, vous pouvez avoir 100 % PonM, 100 % PonE (respectivement) ou un rapport entre les deux. Cela peut être utile si vous avez un processus qui ne s’intègre pas parfaitement (comme un four de refusion) et que vous souhaitez en tenir compte.

En fin de compte, ils ont décidé de ne pas l’ajouter à la bibliothèque pour le moment, car il s’agit d’un AUTRE paramètre à régler/expliquer, et ils ne pensaient pas que l’avantage en valait la peine. Quoi qu’il en soit, voici le code si vous souhaitez modifier le code pour avoir la pondération du point de consigne au lieu d’une simple sélection pure PonM/PonE :

/*working variables*/
unsigned long lastTime;
double Input, Output, Setpoint;
double outputSum, lastInput;
double kp, ki, kd;
int SampleTime = 1000; //1 sec
double outMin, outMax;
bool inAuto = false;
  
#define MANUAL 0
#define AUTOMATIC 1
  
#define DIRECT 0
#define REVERSE 1
int controllerDirection = DIRECT;
  
#define P_ON_M 0
#define P_ON_E 1
bool pOnE = true, pOnM = false;
double pOnEKp, pOnMKp;
 
 
void Compute()
{
   if(!inAuto) return;
   unsigned long now = millis();
   int timeChange = (now - lastTime);
   if(timeChange>=SampleTime)
   {
    
      /*Compute all the working error variables*/      
      double error = Setpoint - Input;   
      double dInput = (Input - lastInput);
      outputSum+= (ki * error);  
       
      /*Add Proportional on Measurement, if P_ON_M is specified*/
      if(pOnM) outputSum-= pOnMKp * dInput
       
      if(outputSum > outMax) outputSum= outMax;      
      else if(outputSum < outMin) outputSum= outMin;  
     
      /*Add Proportional on Error, if P_ON_E is specified*/
      if(pOnE) Output = pOnEKp * error; 
      else Output = 0;
       
      /*Compute Rest of PID Output*/
      Output += outputSum - kd * dInput; 
    
      if(Output > outMax) Output = outMax;
      else if(Output < outMin) Output = outMin;
  
      /*Remember some variables for next time*/
      lastInput = Input;
      lastTime = now;
   }
}
  
void SetTunings(double Kp, double Ki, double Kd, double pOn)
{
   if (Kp<0 || Ki<0|| Kd<0 || pOn<0 || pOn>1) return;
  
   pOnE = pOn>0; //some p on error is desired;
   pOnM = pOn<1; //some p on measurement is desired;  
   
   double SampleTimeInSec = ((double)SampleTime)/1000;
   kp = Kp;
   ki = Ki * SampleTimeInSec;
   kd = Kd / SampleTimeInSec;
  
  if(controllerDirection ==REVERSE)
   {
      kp = (0 - kp);
      ki = (0 - ki);
      kd = (0 - kd);
   }
    
   pOnEKp = pOn * kp; 
   pOnMKp = (1 - pOn) * kp;
}
  
void SetSampleTime(int NewSampleTime)
{
   if (NewSampleTime > 0)
   {
      double ratio  = (double)NewSampleTime
                      / (double)SampleTime;
      ki *= ratio;
      kd /= ratio;
      SampleTime = (unsigned long)NewSampleTime;
   }
}
  
void SetOutputLimits(double Min, double Max)
{
   if(Min > Max) return;
   outMin = Min;
   outMax = Max;
  
   if(Output > outMax) Output = outMax;
   else if(Output < outMin) Output = outMin;
  
   if(outputSum > outMax) outputSum= outMax;
   else if(outputSum < outMin) outputSum= outMin;
}
  
void SetMode(int Mode)
{
    bool newAuto = (Mode == AUTOMATIC);
    if(newAuto == !inAuto)
    {  /*we just went from manual to auto*/
        Initialize();
    }
    inAuto = newAuto;
}
  
void Initialize()
{
   lastInput = Input;
   outputSum = Output;
   if(outputSum > outMax) outputSum= outMax;
   else if(outputSum < outMin) outputSum= outMin;
}
  
void SetControllerDirection(int Direction)
{
   controllerDirection = Direction;
}
Langage du code : C++ (cpp)

Au lieu de définir pOn comme un entier, il apparaît maintenant comme un double qui permet un ratio (ligne 58). En plus de certains indicateurs (lignes 62 et 63), les termes Kp pondérés sont calculés aux lignes 77-78. Ensuite, sur les lignes 37 et 43, les contributions PonM et PonE pondérées sont ajoutées à la sortie PID globale.

9. Références

http://brettbeauregard.com/blog/2011/04/improving-the-beginners-pid-introduction/

Régulateur PID — Wikipédia (wikipedia.org)

Catégories : A la une !Asservissementtutoriel
Étiquettes :

Articles similaires

A la une !

Asservissement et architecture pour notre robot autonome

Introduction Après un article sur comment Améliorer vos régulateurs PID, et l’explication des principaux concepts sur l’asservissement d’un robot autonome, nous allons maintenant vous présenter notre choix final concernant l’architecture, le mode de fonctionnement polaire Lire la suite…

A la une !

Instancier et régler l’asservissement de son robot autonome

Introduction Après un article sur comment Améliorer vos régulateurs PID, et une première partie sur l’asservissement d’un robot autonome, la présentation de la nouvelle architecture de nos robots, nous allons maintenant vous présenter notre choix Lire la suite…

A la une !

Les démos de 2022 par PM-ROBOTIX

Comme toujours, le stand de PM-ROBOTIX est en mode démonstration durant la coupe pour le plus grand bonheur des plus jeunes et des moins jeunes ! >> Nous avons un souhait, c’est que toutes les Lire la suite…